Всем привет. Как всегда расскажут, что это бесполезная статья, как и про системы счисления, но всё же у меня остаётся надежда, что кто-то да задавался вопросом о кватернионах. И да, если нужно больше статьей по математике — пишите, могу разобрать всё, что вам нужно в рамках «адекватной» математики (например, тригонометрию могу разобрать для того, чтобы проще было вам связывать между собой углы и координаты, синусы-косинусы и прочее).
Значит, положение любого объекта в физике (и в компьютерных играх) задаётся неким вектором. В случае трехмерного пространства (3D) у нас трёхмерный вектор, то есть упорядоченный набор из 3 чисел. Пример:
(2, 4.5, -82.11) — это пример координаты. Логика простая: у нас имеется три взаимно перпендикулярных оси (обычно XYZ), и на каждой оси отмечена «единица». Ну и мы стартуем в начале координат и двигаемся вдоль направлений оси на столько этих «единиц» (единичных отрезков), на сколько у нас указано в векторе. Просто для понимания воспринимать следующие направления осей: вверх-вниз, вправо-влево, вперёд-назад. И тогда ясно, что любое положение соответствует какому-либо вектору, а любой вектор соответствует какому-то положению. Более того, разные вектора (координаты) соответствуют разным положениям.И вот это называется в математике «биекция», где мы можем между любой позицией и координатой поставить взаимно однозначное соответствие (то есть можем по координате определить позицию и по позиции определить координату). Именно этого эффекта учёные постарались достичь и при вращении объектов. Если вы задумаетесь над вопросом «а как можно с помощью чисел записать вращение объекта?» — то поймёте, что всё не так просто.
В голову приходит метод вращения вдоль осей (и записывать углы, на которые мы поворачиваем), типа вот так:

Но вы тут поймёте достаточно быстро, что порядок вращения имеет значение (причём неважно — у вас внутренние оси вращаются с объектом или они закреплены на месте), давайте покажу:
Еще одна проблема — если мы будем плавно вращать объект, то вполне возможна ситуация, что углы (это называется углы Эйлера) в какой-то момент резко скакнут, поэтому не выполняется непрерывность, что в математике обычно неприятно (матанализ вообще весь построен на принципе непрерывности). Из этого вытекает следующая проблема: если мы будем вращать объект в той плоскости, в которой мы захотим — непонятно как считать эти углы. С таким подходом мы можем разве что вращать объект в трёх осях (X, Y, Z), и то не в произвольном порядке, что сильно ограничивает нас и сужает круг возможностей (например, при разработке игры при ударе об кочку хотелось бы иметь возможность начать вращать машину так, чтобы задняя часть переворачивалась, но понятное дело, что угол, под которым мы будем подъезжать к кочке, всегда разный, поэтому такой вариант работы [через углы по осям] нам не подходит аж никак).
И спасение есть! Это кватернионы, которые использует GTA SA в том числе (в общем то это единственный известный мне метод, я не думаю, что кто-то использует что-то другое).
То, что это гиперкомплексные числа, вы прочитали, наверное 😀. Но это не помогает разобраться а как же с ними работать и что это такое? Если вкратце, то это число вида «комплексное от комплексного», оно имеет следующий вид:
a + bi + cj + dk, где i, j, k — мнимые единицыПервое правило:
i² = j² = k² = ijk = -1, причём между собой они НЕ равны (это разные буквы и обозначают они разные числа!)А связь между ними такая:
ij = k; jk = i; ki = j;
ji = -k; kj = -i; ik = -j;
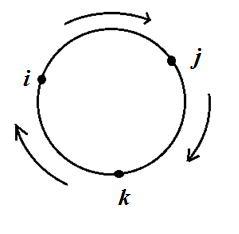
ij = -ji, порядок умножения имеет значение!Не то, чтобы в этом есть какой-то смысл, но Гамильтон, который их изобрёл, как я понимаю, просто подумал «ну вот а что будем, если мы сделаем такие интересные числа?» — и оказалось, что они полезны. Они обладают нужными математическими свойствами (не будем вдаваться в поля и прочее...)
Вот стандартная функция получения кватерниона т/с:
float x, float y, float z, float w = getVehicleQuaternion(Vehicle car)x, y, z и w — это и есть кватернион w + x * i + y * j + z * k.Теперь давайте поговорим о вращении и вообще что связывает эти страшные числа с положениями (поворотами) объектов?
Во-первых, введём понятие вектор нормали.
Так вот вот этот перпендикулярный вектор называется «нормалью к плоскости». У любой плоскости перпендикулярный вектор называется нормалью, она (нормаль) всегда существует и, более того, её легко задать с помощью XYZ-координат вектора. Вращение в плоскости = вращение нормали к этой плоскости как спицы в руках, если совсем наглядно говорить (при таком вращении нормаль вообще не двигается). В дальнейшем плоскость, относительно которой мы вращаем, будем задавать именно этим вектором.
Следующий интересный факт, который надо осознать: любое вращение (переход из любого положения в любое) можно осуществить с помощью вращения всего в одной плоскости. В большинстве случаев это тяжело представить в голове, именно поэтому я начал говорить о нормалях и прочем. Вот простая картинка. Коричневый и зелёный вектора здесь просто для наглядности, чтобы вы понимали в какое положение переходит этот прямоугольник. А вот синий вектор (на картинке справа — вниз, влево, вперед; на картинке слева он же — влево, вперёд, вниз) при таком вращении, как вы можете заметить, не меняется. А это значит, что это нормаль к нашей плоскости! Саму плоскость я рисовать не стал, так как она под углом 45 градусов и крайне неудобно смотрелась бы...
Значит теперь, как вы понимаете, любое вращение можно задать просто задав вектор нормали и угол, на который мы поворачиваем. Ну, строго говоря, у нас еще есть начальное состояние (это так как модельку нарисовал моделлер), а дальше мы её уже крутим-вертим.
Так вот кватернион это и обозначает. Если мы вращаем объект на угол
α «в плоскости», нормаль которой имеет координаты (x, y, z), то кватернион данного вращения будет иметь вид:q = cos(α / 2) + sin(α / 2) * (x * i + y * j + z * k)И в чём же прикол — спросите вы?
Ну, во-первых, вы можете перевернуть машину. Давайте попробуем... выбираем любую плоскость, параллельную вертикальной оси, и выписываем координаты вектора нормали:
(1 / √2; -1 / √2; 0).q = cos(90) + sin(90) * (x * i + y * j + z * k) = 0 + 1 * (x * i + y * j + z * k) = i / √2 - j / √2, а всё остальное сократитсяНу и в виде кода Lua:
Lua:
setVehicleQuaternion(car, 0.707, -0.707, 0, 0)Во-вторых, мы можем вращать последовательно. Сначала повернули в одной плоскости, потом в другой, потом в третьей. Для этого нужно просто перемножать кватернионы.
Давайте перевёрнутую машину попробуем опять поставить на колёса, для этого повернём её же еще раз на 180 градусов в той же плоскости.
И так, мы имеем:
(i / √2 - j / √2) * (i / √2 - j / √2) = 1/2 * (i - j)² = 1/2 * (i² - ij - ji + j²) = (-1 - k - (-k) - 1) / 2 = -1 = -1 + 0i + 0j + 0k.Так, итого надо в виде кода записать:
Lua:
setVehicleQuaternion(car, 0, 0, 0, -1)Поворот вектора на кватернион
Допустим, у нас есть вектор
(x, y, z). Мы хотим повернуть его на кватернион q. Для этого нам надо использовать формулу: v' = q * v * q'. Здесь v — вектор, v' — вектор после поворота, q — кватернион (который описывает наш поворот), q' — сопряжённый кватернион.Сопряжённый кватернион для кватерниона
a + bi + cj + dk — это кватернион a - bi - cj - dk. Просто надо знаки перед i, j, k заменить на противоположные.Давайте это всё на примере. У нас есть три оси: X:
(1, 0, 0), Y: (0, 1, 0), Z: (0, 0, 1). Давайте мы будем поворачивать их на кватернион автомобиля: картинка слева (первая) — без поворота, картинка справа — с поворотом на кватернион авто.(если картинки не показываются, то вот первая, а вот вторая)
В виде кода Lua это выглядит вот так:
Функции:
function quaternion_multiply(a, b, c, d, w, x, y, z)
return a * w - b * x - c * y - d * z, a * x + b * w + c * z - d * y, a * y - b * z + c * w + d * x, a * z + b * y - c * x + d * w
end
function rotate_vector_on_quaternion(x, y, z, a, b, c, d)
-- Вектор v переходит в v' по повороте на кватернион q вот так: v' = q * v * q'
local a1, b1, c1, d1 = quaternion_multiply(a, b, c, d, 0, x, y, z)
local a2, b2, c2, d2 = quaternion_multiply(a1, b1, c1, d1, a, -b, -c, -d)
return b2, c2, d2
end
Lua:
x, y, z, w = getVehicleQuaternion(car)
local ax, bx, cx = rotate_vector_on_quaternion(1, 0, 0, w, x, y, z)
local ay, by, cy = rotate_vector_on_quaternion(0, 1, 0, w, x, y, z)
local az, bz, cz = rotate_vector_on_quaternion(0, 0, 1, w, x, y, z)
local carX, carY, carZ = getCarCoordinates(car)
local wposX1, wposY1 = convert3DCoordsToScreen(carX, carY, carZ)
local wposX2, wposY2 = convert3DCoordsToScreen(carX + ax, carY + bx, carZ + cx)
renderDrawLine(wposX1, wposY1, wposX2, wposY2, 5.0, 0xFFFFFFFF)
local wposX2, wposY2 = convert3DCoordsToScreen(carX + ay, carY + by, carZ + cy)
renderDrawLine(wposX1, wposY1, wposX2, wposY2, 5.0, 0xFFFFFFFF)
local wposX2, wposY2 = convert3DCoordsToScreen(carX + az, carY + bz, carZ + cz)
renderDrawLine(wposX1, wposY1, wposX2, wposY2, 5.0, 0xFFFFFFFF)А теперь кто-то да сможет пофиксить этот долбанный редактор объектов самп, в котором крутишь оси, а нихера не происходит, потому что реализован по тупому)
Постараюсь сам заняться как будет мотивация 😀
И еще вот это моё сообщение причитайте. Там краткий итог статьи.
Последнее редактирование:

